Krull dimension

In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull (1899–1971), is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring.

A field k has Krull dimension 0; more generally, $k[x_1, ..., x_n]$ has Krull dimension n. A principal ideal domain that is not a field has Krull dimension 1.

1 Explanation
2 Krull dimension and schemes
3 Examples
4 Krull Dimension of a Module
5 See also
6 Notes
7 Bibliography

Explanation

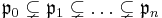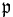We say that a strict chain of inclusions of prime ideals of the form: $\mathfrak{p}_0\subsetneq \mathfrak{p}_1\subsetneq \ldots \subsetneq \mathfrak{p}_n$ is of length n. That is, it is counting the number of strict inclusions, not the number of primes, although these only differ by 1. Given a prime $\mathfrak{p}\subset R$ , we define the height of $\mathfrak{p}$ , written $\operatorname{ht}(\mathfrak{p})$ to be the supremum of the set $\{n\in \mathbb{N}: \mathfrak{p} \text{ is the supremum of a strict chain of length } n \}$

We define the Krull dimension of $R$ to be the supremum of the heights of all of its primes.

Nagata gave an example of a ring that has infinite Krull dimension even though every prime ideal has finite height. Nagata also gave an example of a Noetherian ring where not every chain can be extended to a maximal chain.^[1] Rings in which every chain of prime ideals can be extended to a maximal chain are known as catenary rings.

Krull dimension and schemes

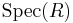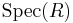It follows readily from the definition of the spectrum of a ring $\operatorname{Spec}(R)$ , the space of prime ideals of $R$ equipped with the Zariski topology, that the Krull dimension of $R$ is precisely equal to the irreducible dimension of its spectrum. This follows immediately from the Galois connection between ideals of $R$ and closed subsets of $\operatorname{Spec}(R)$ and the elementary observation that the prime ideals of $R$ correspond by the definition of the spectrum to the generic points of the closed subsets they to which they correspond under the Galois connection.

Examples

The dimension of a polynomial ring over a field $k[x_1 ,\ldots,x_d]$ is the number of indeterminates. These rings correspond to affine spaces in the language of schemes, so this result can be thought of as foundational. In general, if R is a Noetherian ring, then the dimension of R[x] is d + 1. If the Noetherianity hypothesis is dropped, then R[x] can have dimension anywhere between d + 1 and 2d + 1.

The ring of integers 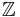$\mathbb Z$ has dimension 1.

An integral domain is a field if and only if its Krull dimension is zero. Dedekind domains that are not fields (for example, discrete valuation rings) have dimension one. In general, a Noetherian ring is Artinian if and only if its Krull dimension is 0.

Krull Dimension of a Module

If R is a commutative ring, and M is an R-module, we define the Krull dimension of M to be the Krull dimension of the quotient of R making M a faithful module. That is, we define it by the formula:

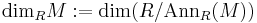
$\operatorname{dim}_R M�:= \operatorname{dim}( R/\operatorname{Ann}_R(M))$

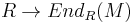where $\operatorname{Ann}_R(M)$ , the annihilator, is the kernel of the natural map $R\to End_R(M)$ of R into the ring of $R$ -linear endomorphisms on $M$ .

In the language of schemes, finite type modules are interpreted as coherent sheaves, or generalized finite rank vector bundles.

Notes

^ Nagata, M. Local Rings (1962). Wiley, New York.

Bibliography

Irving Kaplansky, Commutative rings (revised ed.), University of Chicago Press, 1974, ISBN 0-226-42454-5. Page 32.
A.I. Kostrikin and I.R. Shafarevich (edd), Algebra II, Encyclopaedia of Mathematical Scieinces 18, Springer-Verlag, 1991, ISBN 3-540-18177-6. Sect.4.7.